Радона формула: Преобразование Радона — Википедия – XuMuK.ru — РАДОН

Содержание

Преобразование Радона — Википедия

Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917-го года^[1].

Важнейшее свойство преобразования Радона — обратимость, то есть возможность восстанавливать исходную функцию по её преобразованию Радона.

Двумерное преобразование Радона.
В данном случае R(s,α) есть интеграл от f(x,y) вдоль прямой AA^‘

Рассмотрение преобразования Радона удобно начать с простейшего случая функции двух переменных, к тому же, именно этот случай наиболее практически важен.

Пусть f(x,y){\displaystyle f(x,y)} функция двух действительных переменных, определённая на всей плоскости и достаточно быстро убывающая на бесконечности (так, чтобы соответствующие несобственные интегралы сходились). Тогда преобразованием Радона функции f(x,y){\displaystyle f(x,y)} называется функция

R(s,α)=∫−∞∞f(scos⁡α−zsin⁡α,ssin⁡α+zcos⁡α)dz{\displaystyle R(s,\alpha )=\int \limits _{-\infty }^{\infty }f(s\cos \alpha -z\sin \alpha ,s\sin \alpha +z\cos \alpha )dz} (1)

Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной вектору n→=(cos⁡α,sin⁡α){\displaystyle {\vec {n}}=(\cos \alpha ,\sin \alpha )} и проходящей на расстоянии s{\displaystyle s} (измеренного вдоль вектора n→{\displaystyle {\vec {n}}}, с соответствующим знаком) от начала координат.

Связь преобразования Радона и преобразования Фурье. Формула обращения[править | править код]

Рассмотрим двумерное преобразование Фурье от функции f(x,y){\displaystyle f(x,y)}

F(kx,ky)=∫−∞∞∫−∞∞f(x,y)e−i(kxx+kyy)dxdy{\displaystyle F(k_{x},k_{y})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)e^{-i(k_{x}x+k_{y}y)}dxdy} (2)

Можно заметить, что показатель экспоненты в этом интеграле не изменяется, если мы двигаемся вдоль прямой, перпендикулярной вектору k→=(kx,ky){\displaystyle {\vec {k}}=(k_{x},k_{y})}, и изменяется наиболее быстро, если мы движемся вдоль этого вектора. Поэтому удобно перейти к новым переменным. Обозначим k→=(kx,ky)=ω(cos⁡α,sin⁡α){\displaystyle {\vec {k}}=(k_{x},k_{y})=\omega (\cos \alpha ,\sin \alpha )}, мы выберем новые переменные s=xcos⁡α+ysin⁡α,{\displaystyle s=x\cos \alpha +y\sin \alpha ,} z=−xsin⁡α+ycos⁡α{\displaystyle z=-x\sin \alpha +y\cos \alpha }. Сделав замену переменных в интеграле, получаем

F(ωcos⁡α,ωsin⁡α)=∫−∞∞(∫−∞∞f(scos⁡α−zsin⁡α,ssin⁡α+zcos⁡α)e−iωsdz)ds{\displaystyle F(\omega \cos \alpha ,\omega \sin \alpha )=\int \limits _{-\infty }^{\infty }\left(\int \limits _{-\infty }^{\infty }f(s\cos \alpha -z\sin \alpha ,s\sin \alpha +z\cos \alpha )e^{-i\omega s}dz\right)ds}

т.е.

F(ωcos⁡α,ωsin⁡α)=∫−∞∞e−iωsR(s,α)ds{\displaystyle F(\omega \cos \alpha ,\omega \sin \alpha )=\int \limits _{-\infty }^{\infty }e^{-i\omega s}R(s,\alpha )ds} (3)

Таким образом, одномерное преобразование Фурье от преобразования Радона для функции f(x,y){\displaystyle f(x,y)} есть не что иное как двумерное преобразование Фурье от функции f(x,y){\displaystyle f(x,y)}. Поскольку преобразование Фурье функции f(x,y){\displaystyle f(x,y)} существует (это необходимое исходное допущение), то существует и обратное преобразование Фурье от функции F(ωcos⁡α,ωsin⁡α){\displaystyle F(\omega \cos \alpha ,\omega \sin \alpha )}. Учитывая (3), можно заключить, что должно существовать и обратное преобразование Радона.

Формула обращения для двумерного преобразования Фурье, как известно, выглядит следующим образом

f(x,y)=1(2π)2∫−∞∞∫−∞∞F(kx,ky)ei(kxx+kyy)dkxdky.{\displaystyle f(x,y)={\frac {1}{(2\pi )^{2}}}\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }F(k_{x},k_{y})e^{i(k_{x}x+k_{y}y)}dk_{x}dk_{y}.}

Для наших целей удобно переписать эту формулу в полярных координатах

f(x,y)=1(2π)2∫0∞∫02πeiω(xcos⁡α+ysin⁡α)F(ωcos⁡α,ωsin⁡α)ωdαdω{\displaystyle f(x,y)={\frac {1}{(2\pi )^{2}}}\int \limits _{0}^{\infty }\int \limits _{0}^{2\pi }e^{i\omega (x\cos \alpha +y\sin \alpha )}F(\omega \cos \alpha ,\omega \sin \alpha )\omega d\alpha d\omega },

что, учитывая (3), немедленно даёт формулу обратного преобразования Радона

f(x,y)=1(2π)2∫02π∫0∞eiω(xcos⁡α+ysin⁡α) R~(ω,α)ωdωdα{\displaystyle f(x,y)={\frac {1}{(2\pi )^{2}}}\int \limits _{0}^{2\pi }\int \limits _{0}^{\infty }e^{i\omega (x\cos \alpha +y\sin \alpha )}\ {\tilde {R}}(\omega ,\alpha )\omega d\omega d\alpha } (4),

где R~(ω,α)=∫−∞∞R(s,α)e−iωsds{\displaystyle {\tilde {R}}(\omega ,\alpha )=\int \limits _{-\infty }^{\infty }R(s,\alpha )e^{-i\omega s}ds}.

Выражение (4), помимо того что является одним из вариантов записи обратного преобразования Радона, также определяет метод реконструкции f(x,y){\displaystyle f(x,y)} из её проекций R(s,αi){\displaystyle R(s,\alpha _{i})}, называемый специалистами методом Фурье-синтеза. Таким образом, в методе Фурье-синтеза сначала необходимо сформировать из большого количества одномерных Фурье-образов проекций по полярной сетке R~(ω,αi){\displaystyle {\tilde {R}}(\omega ,\alpha _{i})} двумерный спектр R~(ω,α){\displaystyle {\tilde {R}}(\omega ,\alpha )} (при этом используется теорема о центральном сечении), а затем выполнить обратное двумерное преобразование Фурье в полярной системе координат от R~(ω,α){\displaystyle {\tilde {R}}(\omega ,\alpha )}. Существуют и другие методы реконструкции f(x,y){\displaystyle f(x,y)} из R(s,α){\displaystyle R(s,\alpha )} ^[2]

Теорема о центральном сечении[править | править код]

Применим операцию прямого преобразования Фурье к преобразованию Радона от f(x,y){\displaystyle f(x,y)}:

∫−∞∞R(s,α)e−iωsds={\displaystyle \int \limits _{-\infty }^{\infty }R(s,\alpha )e^{-i\omega s}ds=} ∫−∞∞(∫−∞∞∫−∞∞f(x,y)δ(s−xcos⁡α−ysin⁡α)dxdy)e−iωsds{\displaystyle \int \limits _{-\infty }^{\infty }\left(\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)\delta (s-x\cos \alpha -y\sin \alpha )dxdy\right)e^{-i\omega s}ds}

Перестановка порядка интегрирования и применение фильтрующего свойства дельта функции приводят к формулировке теоремы о центральном сечении:

∫−∞∞R(s,α)e−iωsds={\displaystyle \int \limits _{-\infty }^{\infty }R(s,\alpha )e^{-i\omega s}ds=} ∫−∞∞∫−∞∞(∫−∞∞e−iωsδ(s−xcos⁡α−ysin⁡α))ds)f(x,y)dxdy=∫−∞∞∫−∞∞f(x,y)e−iω(xcos⁡α+ysin⁡α)dxdy{\displaystyle \int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }\left(\int \limits _{-\infty }^{\infty }e^{-i\omega s}\delta (s-x\cos \alpha -y\sin \alpha ))ds\right)f(x,y)dxdy=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)e^{-i\omega (x\cos \alpha +y\sin \alpha )}dxdy}

Из последнего равенства, в частности, следует, что Фурье-образ проекции R(s,α){\displaystyle R(s,\alpha )} представляет собой спектр функции f(x,y){\displaystyle f(x,y)} вдоль прямой, проходящей через начало координат в частотной плоскости под углом α+π/2{\displaystyle \alpha +\pi /2}. Таким образом Фурье-образ проекции является центральным сечением двумерного Фурье-образа функции f(x,y){\displaystyle f(x,y)}. В литературе это свойство называют теоремой о центральном слое или центральном сечении.

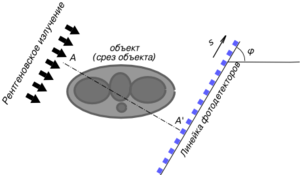Схема получения рентгеновской томограммы

В компьютерной рентгеновской томографии линейка детекторов измеряет поглощение исследуемым объектом параллельного пучка излучения (например, рентгеновских лучей в медицинской томографии, сейсмических волн в геофизической томографии). В соответствии с законом Бугера-Ламберта-Бера интенсивность излучения, измеряемая детектором в точке s линейки пропорциональна exp⁡{−∫AA′ρ(x,y)dz}{\displaystyle \exp \left\{-\int \limits _{AA’}\rho (x,y)dz\right\}}, где ρ(x,y){\displaystyle \rho (x,y)} показатель поглощения вещества объекта для данного типа излучения, а интеграл берётся вдоль прямой AA′{\displaystyle AA’} проходящей через данный детектор и перпендикулярной линейке детекторов (z — координата на этой прямой). Соответственно, логарифм от интенсивности, взятый с обратным знаком, даёт преобразование Радона от показателя поглощения. Вращая систему из источника излучения и детектора вокруг объекта (при этом оставаясь в одной плоскости), или вращая сам объект вокруг оси, перпендикулярной плоскости, показаной на рисунке, получают множество луч-сумм в выбранном срезе объекта. Затем, используя один из методов реконструкции, можно восстановить распределение показателя поглощения в любой точке прозондированной плоскости объекта.

Преобразования Радона подобным образом используются и в магнито-резонансной томографии

[3].

Преобразование Радона для функции произвольного числа переменных[править | править код]

Преобразование Радона для функции двух переменных можно удобно переписать через интеграл по всему пространству с помощью дельта-функции Дирака:

R(s,n→)=∫δ(n→r→−s)f(r→)dr→{\displaystyle R(s,{\vec {n}})=\int \delta ({\vec {n}}{\vec {r}}-s)f({\vec {r}})d{\vec {r}}} (2)

Здесь мы обозначили r→=(x,y){\displaystyle {\vec {r}}=(x,y)} — радиус-вектор из начала координат, dr→=dxdy{\displaystyle d{\vec {r}}=dxdy} — двумерный элемент объёма, n→{\displaystyle {\vec {n}}} — единичный вектор, который можно параметризовать как n→=(cos⁡α,sin⁡α){\displaystyle {\vec {n}}=(\cos \alpha ,\sin \alpha )}. С помощью замены переменных легко убедиться, что определения преобразования Радона (1) и (2) полностью идентичны.

Формула (2) тривиально обобщается на случай произвольного числа измерений, для этого её даже не надо переписывать, достаточно под r→{\displaystyle {\vec {r}}}, dV{\displaystyle dV} и n→{\displaystyle {\vec {n}}} понимать соответственно N{\displaystyle N}-мерный радиус-вектор из начала координат, элемент объёма в N{\displaystyle N}-мерном пространстве и N{\displaystyle N}-мерный единичный вектор. В принципе, вектор n→{\displaystyle {\vec {n}}} можно параметризовать углами в пространстве любого числа измерений. Например, в трёхмерном пространстве имеется параметризация n→=(sin⁡θcos⁡α,sin⁡θsin⁡α,cos⁡θ){\displaystyle {\vec {n}}=(\sin \theta \cos \alpha ,\sin \theta \sin \alpha ,\cos \theta )}.

Геометрический смысл преобразования Радона в многомерном случае: интеграл от функции по гиперплоскости, перпендикулярной вектору n→{\displaystyle {\vec {n}}} и проходящей на расстоянии s{\displaystyle s} от начала координат (взятом со знаком минус, если перпендикуляр из начала координат на плоскость противоположно направлен с вектором n→{\displaystyle {\vec {n}}}).

Обращение многомерного преобразования Радона[править | править код]

В многомерном случае преобразование Радона достаточно хорошей функции тоже обратимо. Покажем это.

Рассмотрим преобразование Фурье от R(s,n→){\displaystyle R(s,{\vec {n}})} по переменной s{\displaystyle s}, то есть

∫R(s,n→)e−isωds{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds}.

Используя формулу (2) и свойства дельта-функции мы получим

∫R(s,n→)e−isωds=∫f(r→)e−ir→n→ωdr→{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds=\int f({\vec {r}})e^{-i{\vec {r}}{\vec {n}}\omega }d{\vec {r}}}.

Заметим теперь, что ∫0∞ωN−1dω∫dn→{\displaystyle \int \limits _{0}^{\infty }\omega ^{N-1}d\omega \int d{\vec {n}}} есть интеграл по всему N{\displaystyle N}-мерному пространству (здесь под интегралом ∫dn→{\displaystyle \int d{\vec {n}}} подразумевается интеграл по (N−1){\displaystyle (N-1)}-мерной сфере, в частности, для N=2{\displaystyle N=2} ∫dn→=∫dα{\displaystyle \int d{\vec {n}}=\int \limits d\alpha }, для N=3{\displaystyle N=3} ∫dn→=∫dϕcos⁡θdθ{\displaystyle \int d{\vec {n}}=\int \limits d\phi \cos \theta d\theta }). Из этого следует, что

∫0∞ωN−1dω(2π)N∫dn→ei(r→′−r→)ωn→=δ(r→−r→′){\displaystyle \int \limits _{0}^{\infty }{\frac {\omega ^{N-1}d\omega }{(2\pi )^{N}}}\int d{\vec {n}}e^{i({\vec {r}}’-{\vec {r}})\omega {\vec {n}}}=\delta ({\vec {r}}-{\vec {r}}’)}.

Используя это представление векторной дельта-функции, получаем формулу обращения

f(r→′)=∫dn→∫0∞ωN−1dω(2π)Neir→′n→ω∫dse−isωR(s,n→){\displaystyle f({\vec {r}}’)=\int d{\vec {n}}\int \limits _{0}^{\infty }{\frac {\omega ^{N-1}d\omega }{(2\pi )^{N}}}e^{i{\vec {r}}'{\vec {n}}\omega }\int dse^{-is\omega }R(s,{\vec {n}})}.

↑ J. Radon. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten // Berichte Sächsische Akademie der Wissenschaften, Bande 29, s. 262-277, Leipzig, 1917.
↑ Глава 1 (неопр.) (недоступная ссылка). Дата обращения 15 октября 2012. Архивировано 18 сентября 2010 года.
↑ S.R. Deans, S.Roderick «The Radon Transform and Some of its Applications» Wilwy, New York, 1983 (англ.)

И.С.Грузман Математические задачи компьютерной томографии. Соросовский образовательный журнал No. 5, 2001 ^pdf^{txt (недоступная ссылка)}
Deans, Stanley R., The Radon Transform and Some of Its Applications. New York: John Wiley & Sons, 1983.
Natterer, Frank, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1
Natterer, Frank and Frank Wubbeling, Mathematical Methods in Image Reconstruction. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-472-9

Радон

Радо́н — элемент главной подгруппы восьмой группы, шестого периода периодической системы химических элементов Д. И. Менделеева, с атомным номером 86. Обозначается символом Rn (Radon). Простое вещество радон (CAS-номер: 10043-92-2) в нормальных условиях — бесцветный инертный газ; радиоактивен, может представлять опасность для здоровья и жизни. При комнатной температуре является одним из самых тяжелых газов. Наиболее стабильный изотоп (²²²Rn) имеет период полураспада 3,8 суток.

История открытия и происхождение названия

Английский ученый Э. Резерфорд в 1899 году отметил, что препараты тория испускают, кроме α-частиц, и некое неизвестное ранее вещество, так что воздух вокруг препаратов тория постепенно становится радиоактивным. Это вещество он предложил назвать эмана́цией (от латинского emanatio — истечение) тория и дать ему символ Em. Последующие наблюдения показали, что и препараты радия также испускают некую эманацию, которая обладает радиоактивными свойствами и ведет себя как инертный газ. Первоначально эманацию тория называли торо́ном, а эманацию радия — радо́ном. Было доказано, что все эманации на самом деле представляют собой радионуклиды нового элемента — инертного газа, которому отвечает атомный номер 86. Впервые его выделили в чистом виде Рамзай и Грей в 1908 году, они же предложили назвать газ нитон (от лат. nitens, светящийся). В 1923 году газ получил окончательное название радон и символ Em был сменен на Rn.

Получение

Для получения радона через водный раствор любой соли радия продувают воздух, который уносит с собой образующийся при радиоактивном распаде радия радон. Далее воздух тщательно фильтруют для отделения микрокапель раствора, содержащего соль радия, которые могут быть захвачены током воздуха. Для получения собственно радона из смеси газов удаляют химически активные вещества (кислород, водород, водяные пары и т. д.), остаток конденсируют жидким азотом, затем из конденсата отгоняют азот и другие инертные газы (аргон, неон и т.д).

Физические свойства

Радон — радиоактивный одноатомный газ без цвета и запаха. Растворимость в воде 460 мл/л; в органических растворителях, в жировой ткани человека растворимость радона в десятки раз выше, чем в воде. Газ хорошо просачивается сквозь полимерные плёнки. Легко адсорбируется активированным углем и силикагелем. Собственная радиоактивность радона вызывает его флюоресценцию. Газообразный и жидкий радон флюоресцирует голубым светом, у твёрдого радона при охлаждении до азотных температур цвет флюоресценции становится сперва жёлтым, затем красно-оранжевым. Цвет свечения в газовом разряде у радона — синий, так как в видимой части спектра радона особо выделяются 8 линий, отвечающих длинам волн от 3982 до 5085 А и лежащих главным образом в синей части спектра, однако из-за отсутствия стабильных изотопов применение его в газосветных приборах невозможно.

Химические свойства

«Благородный газ». Однако радон является наиболее активным благородным газом в химическом отношении, так как его валентные электроны находятся на максимальном удалении от ядра. Радон образует клатраты, которые, хотя и имеют постоянный состав, химических связей с участием атомов радона в них нет. С фтором радон при высоких температурах образует соединения состава RnF_n, где n = 4, 6, 2. Так, дифторид радона RnF₂ является белым нелетучим кристаллическим веществом. Фториды радона могут быть получены также под действием фторирующих агентов (например, фторидов галогенов). При гидролизе тетрафторида RnF₄ и гексафторида RnF₆ образуется оксид радона RnO₃. Получены также соединения с катионом RnF⁺.

Источник: Википедия

Другие заметки по химии

Преобразование Радона — Википедия

Преобразование Радона

— интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917-го года^[1].

Двумерное преобразование Радона

Двумерное преобразование Радона.
В данном случае R(s,α) есть интеграл от f(x,y) вдоль прямой AA^‘

R(s,α)=∫−∞∞f(scos⁡α−zsin⁡α,ssin⁡α+zcos⁡α)dz{\displaystyle R(s,\alpha )=\int \limits _{-\infty }^{\infty }f(s\cos \alpha -z\sin \alpha ,s\sin \alpha +z\cos \alpha )dz} (1)

Связь преобразования Радона и преобразования Фурье. Формула обращения

Рассмотрим двумерное преобразование Фурье от функции f(x,y){\displaystyle f(x,y)}

F(kx,ky)=∫−∞∞∫−∞∞f(x,y)e−i(kxx+kyy)dxdy{\displaystyle F(k_{x},k_{y})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)e^{-i(k_{x}x+k_{y}y)}dxdy} (2)

т.е.

F(ωcos⁡α,ωsin⁡α)=∫−∞∞e−iωsR(s,α)ds{\displaystyle F(\omega \cos \alpha ,\omega \sin \alpha )=\int \limits _{-\infty }^{\infty }e^{-i\omega s}R(s,\alpha )ds} (3)

Формула обращения для двумерного преобразования Фурье, как известно, выглядит следующим образом

Для наших целей удобно переписать эту формулу в полярных координатах

что, учитывая (3), немедленно даёт формулу обратного преобразования Радона

где R~(ω,α)=∫−∞∞R(s,α)e−iωsds{\displaystyle {\tilde {R}}(\omega ,\alpha )=\int \limits _{-\infty }^{\infty }R(s,\alpha )e^{-i\omega s}ds}.

Теорема о центральном сечении

Применим операцию прямого преобразования Фурье к преобразованию Радона от f(x,y){\displaystyle f(x,y)}:

Применение преобразования Радона

Схема получения рентгеновской томограммы

Преобразования Радона подобным образом используются и в магнито-резонансной томографии^[3].

Преобразование Радона для функции произвольного числа переменных

R(s,n→)=∫δ(n→r→−s)f(r→)dr→{\displaystyle R(s,{\vec {n}})=\int \delta ({\vec {n}}{\vec {r}}-s)f({\vec {r}})d{\vec {r}}} (2)

Обращение многомерного преобразования Радона

В многомерном случае преобразование Радона достаточно хорошей функции тоже обратимо. Покажем это.

Рассмотрим преобразование Фурье от R(s,n→){\displaystyle R(s,{\vec {n}})} по переменной s{\displaystyle s}, то есть

∫R(s,n→)e−isωds{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds}.

Используя формулу (2) и свойства дельта-функции мы получим

∫R(s,n→)e−isωds=∫f(r→)e−ir→n→ωdr→{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds=\int f({\vec {r}})e^{-i{\vec {r}}{\vec {n}}\omega }d{\vec {r}}}.

Используя это представление векторной дельта-функции, получаем формулу обращения

Смотри также

Примечания

↑ J. Radon. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten // Berichte Sächsische Akademie der Wissenschaften, Bande 29, s. 262-277, Leipzig, 1917.
↑ Глава 1
↑ S.R. Deans, S.Roderick «The Radon Transform and Some of its Applications» Wilwy, New York, 1983 (англ.)

Ссылки

И.С.Грузман Математические задачи компьютерной томографии. Соросовский образовательный журнал No. 5, 2001 ^pdf^txt
Deans, Stanley R., The Radon Transform and Some of Its Applications. New York: John Wiley & Sons, 1983.
Natterer, Frank, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1
Natterer, Frank and Frank Wubbeling, Mathematical Methods in Image Reconstruction. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-472-9

См. также

Преобразование Радона — это… Что такое Преобразование Радона?

Двумерное преобразование Радона

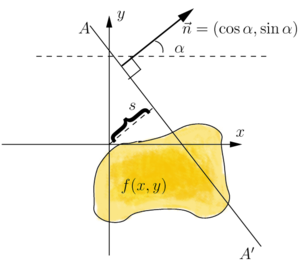Двумерное преобразование Радона.
В данном случае R(s,α) есть интеграл от f(x,y) вдоль прямой AA^‘

Пусть функция двух действительных переменных, определённая на всей плоскости и достаточно быстро убывающая на бесконечности (так, чтобы соответствующие несобственные интегралы сходились). Тогда преобразованием Радона функции называется функция

(1)

Преобразование Радона имеет простой геометрический смысл — это интеграл от функции вдоль прямой, перпендикулярной вектору и проходящей на расстоянии s (измеренного вдоль вектора , с соответствующим знаком) от начала координат.

Связь преобразования Радона и преобразования Фурье. Формула обращения

Рассмотрим двумерное преобразование Фурье от функции

(2)

Можно заметить, что показатель экспоненты в этом интеграле не изменяется, если мы двигаемся вдоль прямой перпендикулярной вектору , и изменяется наиболее быстро если мы движемся вдоль этого вектора. Поэтому удобно перейти к новым переменным. Обозначим , мы выберем новые переменные . Сделав замену переменных в интеграле, получаем

т.е.

(3)

Таким образом, одномерное преобразование Фурье от преобразования Радона для функции есть не что иное как двумерное преобразование Фурье от функции . Поскольку преобразование Фурье функции существует (это необходимое исходное допущение), то существует и обратное преобразование Фурье от функции . Учитывая (3), можно заключить, что должно существовать и обратное преобразование Радона.

Формула обращения для двумерного преобразования Фурье, как известно, выглядит следующим образом

Для наших целей удобно переписать эту формулу в полярных координатах

что, учитывая (3), немедленно даёт формулу обратного преобразования Радона

(4),

где .

Выражение (4), помимо того что является одним из вариантов записи обратного преобразования Радона, также определяет метод реконструкции из её проекций , называемый специалистами методом Фурье-синтеза. Таким образом, в методе Фурье-синтеза сначала необходимо сформировать из большого количества одномерных Фурье-образов проекций по полярной сетке двумерный спектр (при этом используется теорема о центральном сечении), а затем выполнить обратное двумерное преобразование Фурье в полярной системе координат от . Существуют и другие методы реконструкции из ^[2]

Теорема о центральном сечении

Применим операцию прямого преобразования Фурье к преобразованию Радона от :

Из последнего равенства, в частности, следует, что Фурье-образ проекции представляет собой спектр функции вдоль прямой, проходящей через начало координат в частотной плоскости под углом . Таким образом Фурье-образ проекции является центральным сечением двумерного Фурье-образа функции . В литературе это свойство называют теоремой о центральном слое или центральном сечении.

Применение преобразования Радона

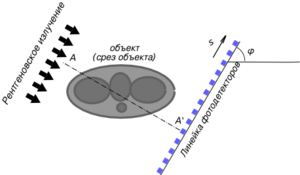Схема получения рентгеновской томограммы

В компьютерной рентгеновской томографии линейка детекторов измеряет поглощение исследуемым объектом параллельного пучка излучения (например, рентгеновских лучей в медицинской томографии, сейсмических волн в геофизической томографии). В соответствии с законом Бугера-Ламберта-Бера интенсивность излучения, измеряемая детектором в точке s линейки пропорциональна , где показатель поглощения вещества объекта для данного типа излучения, а интеграл берётся вдоль прямой проходящей через данный детектор и перпендикулярной линейке детекторов (z — координата на этой прямой). Соответственно, логарифм от интенсивности, взятый с обратным знаком, даёт преобразование Радона от показателя поглощения. Вращая систему из источника излучения и детектора вокруг объекта (при этом оставаясь в одной плоскости), или вращая сам объект вокруг оси, перпендикулярной плоскости, показаной на рисунке, получают множество луч-сумм в выбранном срезе объекта. Затем, используя один из методов реконструкции, можно восстановить распределение показателя поглощения в любой точке прозондированной плоскости объекта.

Преобразование Радона для функции произвольного числа переменных

(2)

Здесь мы обозначили — радиус-вектор из начала координат, — двумерный элемент объёма, — единичный вектор, который можно параметризовать как . С помощью замены переменных легко убедиться, что определения преобразования Радона (1) и (2) полностью идентичны.

Формула (2) тривиально обобщается на случай произвольного числа измерений, для этого её даже не надо переписывать, достаточно под , и понимать соответственно N-мерный радиус-вектор из начала координат, элемент объёма в N-мерном пространстве и N-мерный единичный вектор. В принципе, вектор можно параметризовать углами в пространстве любого числа измерений. Например, в трёхмерном пространстве имеется параметризация .

Геометрический смысл преобразования Радона в многомерном случае: интеграл от функции по гиперплоскости перпендикулярной вектору и проходящей на расстоянии s от начала координат (взятом со знаком минус если перпендикуляр из начала координат на плоскость противоположно направлен с вектором ).

Обращение многомерного преобразования Радона

В многомерном случае преобразование Радона достаточно хорошей функции тоже обратимо. Покажем это.

Рассмотрим преобразование Фурье от по переменной s, то есть

Используя формулу (2) и свойства дельта-функции мы получим

Заметим теперь, что есть интеграл по всему N-мерному пространству (здесь под интегралом подразумевается интеграл по N-1 мерной сфере, в частности, для N=2 , для N=3 ). Из этого следует, что

Используя это представление векторной дельта-функции получаем формулу обращения

Примечания

↑ J. Radon. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten // Berichte Sächsische Akademie der Wissenschaften, Bande 29, s. 262-277, Leipzig, 1917.
↑ Глава 1

Ссылки

И.С.Грузман Математические задачи компьютерной томографии. Соросовский образовательный журнал No. 5, 2001 ^pdf^txt
Deans, Stanley R., The Radon Transform and Some of Its Applications. New York: John Wiley & Sons, 1983.
Natterer, Frank, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1
Natterer, Frank and Frank Wubbeling, Mathematical Methods in Image Reconstruction. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-472-9

См. также

Радон химические свойства — Знаешь как

Химическое поведение молекулы любого изотопа радона определяется его принадлежностью к инертным газам. Правда , в их ряду он наименее благороден легче, чем ксенон, вступает в химическую связь с кислородом, фтором, возможно его взаимодействие и с другими галогенами, но этим, по-видимому, химические реакции его электронной оболочки исчерпываются.

Есть, однако, у радона другая сторона химического поведения, обусловленная неустойчивостью ядра, выбрасывающего при распаде частицы высоких энергий. Эти частицы химически воздействуют на многие встречные вещества, возбуждая и ионизируя молекулы и их осколки. В общем характер воздействия здесь такой же, как у α-частиц, но более многосторонний и резче выраженный. Ведь дочерние продукты в активном осадке испускают еще β— и γ-лучи, длина пробега которых много больше, чем α-частиц. Оттого радиация радона вызывает у стекла, фарфора, минералов глубокое окрашивание. Она разлагает воду на водород, кислород и озон, под действием радона окись углерода в присутствии водорода образует муравьиную кислоту, затем превращающуюся в метан, метан и этан переходят в более высокие предельные углеводороды, ацетилен полимеризуется, вазелин и парафин разрушаются с выделением газов и т. д.

В темноте радон светится за счет энергии распада. Часть энергии выделяется в виде тепла: 1 кюри радона выделяет 28,6 кал в час, следовательно, 1 г радона дает ежемесячно 4400 ккал тепла. Если бы существовали условия для концентрирования радона в толщах земной коры даже в количествах, измеряемых литрами, то радиогенным теплом можно было бы расплавить окружающие горные породы. По этой же причине у исследователя возникла бы необходимость предохранять от расплавления сосуды для хранения сколько-нибудь существенных количеств радона. Изучением радона занималось немало ученых, но и теперь о нем известно меньше, чем о других инертных газах. Довольно полно и точно измерены константы газообразного радона: по физическим свойствам радон, торон и актинон не отличаются от других газов, находящихся в состоянии сильного разрежения. Хуже обстоит дело с константами жидкого и твердого радона, так как очень трудно получить чистый продукт, а в мизерно малых его количествах наличие примесей вызывает существенные искажения результатов исследования. Немалые затруднения доставляет и чрезвычайная токсичность радона . Показательна дискуссия о точке плавления радона. Принятая величина —71° С подвергается сомнению. Одни авторы считают ее равной —65° С, другие —ниже чем —71°. Велики расхождения и в оценке точки кипения. Еще меньше изучен кристаллический радон.

Радон тяжелее гелия в 55 раз и воздуха — в 7,6 раза. Один литр этого газа весил бы почти 10 г. Радон вдвое лучше ксенона и вчетверо лучше криптона растворим в воде. Введя газ в сосуд, заполненный равными объемами воды и воздуха, можно обнаружить, что при комнатной температуре четвертая часть радона окажется в воде, а три четверти — в воздухе; при 0° С половина радона растворится в воде. Даже при 100° С около 10% радона остается в воде. В присутствии электролитов растворимость газа снижается. Это одна из причин пониженного содержания радона в Морской воде по сравнению с речной. Растворимость радона в спиртах и органических кислотах в 20—40 раз лучше, чем в воде. Еще более значительна его растворимость в бензоле, гексане, диэтиловом эфире и хлороформе.

Некоторые твердые вещества — жиры, каучук, парафин, кварц, платина — энергично поглощают радон. Особенно хорошо его адсорбируют силикагель и активный уголь. Последний уже при обычной температуре поглощает практически весь радон и выделяет его обратно лишь при 300°. Стекло и полированный металл при обычной температуре не адсорбируют радон, но быстро конденсируют его, будучи охлажденными до нескольких десятков градусов ниже нуля.

Спектр радона похож на спектр ксенона. В нем известно около 150 линий между 7450 и 3600 А и свыше 100 линий в ультрафиолетовой части.- Наиболее яркие линии на видимом участке приходятся на желтую и зелено-голубую части спектра. С течением времени на спектр радона все более накладывается спектр гелия, и приблизительно через месяц последний полностью перекрывает первый. В газообразном состоянии радон светится ярким голубоватым светом.

Жидкий радон вначале бесцветен и прозрачен, далее мутнеет от продуктов распада. Он вызывает зеленую флюоресценцию стеклянных стенок сосуда. В твердом состоянии радон непрозрачен и светится, по сообщениям некоторых исследователей, как голубой бриллиант. Другие экспериментаторы оценивают его свет как яркий сине-стальной, третьи видели его красноватым.

Вероятно, тут играет роль степень чистоты радона. Плотность жидкого радона — 6,6, твердого — 8,04 г/см³. Их теплота парообразования равна соответственно 19,2 и 20,7 кал/г.

Выше говорилось, что под воздействием межмолекулярных сил сцепления инертные газы образуют малоустойчивые комплексные соединения с нейтральным ядром и дипольными молекулами во внешней сфере. Радон — наиболее реакционноспособный член семейства, поскольку его молекула относительно легче деформируема. Впервые это свойство радона исследовал Б. А. Никитин, получивший его клатратные соединения с водой, фенолом, n-хлорфенолом, толуолом. Ученый показал, что по склонности давать клатратные соединения радон занимает одно из первых мест среди газов. Если бы имелась возможность оперировать большими количествами радона, то достаточно было бы пропустить ток этого газа через воду при обычных температуре и давлении, чтобы тотчас же выпал кристаллический порошок гидрата Rn·6h3O. Но как осадить микродозы радона?

Никитин нашел остроумный выход. Он осаждал радон совместно с изоморфным ему веществом (двуокисью серы, сероводородом), исходя из правила, что если два вещества изоморфны, то их однотипные молекулярные соединения также изоморфны и способны давать смешанные кристаллы. Действительно, практика подтвердила, что в присутствии большого количества изоморфного вещества радон полностью переходит в смешанные кристаллы гидратов или фенолятов. Этим способом удается связать и перевести в осадок ничтожно малые количества радона.

При всей незначительности сильно колеблющихся концентраций радона в атмосфере этот газ мог сыграть заметную роль в эволюции жизни на планете — и как постоянный компонент радиоактивного фона Земли, и как главный фактор ионизации воздуха. По современным представлениям именно умеренная ионизация наряду с малыми концентрациями озона в воздухе и определяет «свежесть» воздуха, его физиологическую благотворность для высших организмов.

Если бы в природе существовали большие скопления радона, то это вызвало бы необходимость защиты всего живого от его губительного действия . Высокая токсичность правлена не самой молекулой радона, а интенсивным потоком α-, β— и γ-лучей, возникающим при распаде радона и его дочерних элементов. Продукты распада оседают в организме в виде тончайшего налета. Наибольшее токсическое действие оказывают α-частицы, несмотря на то, что в мягких тканях тела их пробег составляет только 45—60 мк. При равных дозах облучения биологическая эффективность их в 10—20 раз выше, чем β— и γ-излучений, хотя проникающая способность последних намного сильнее. Дело в том, что плотность ионизации α-излучения на два и три порядка больше плотности ионизации β— и γ-излучений.

Действие радона на организм разносторонне. Главное воздействие он оказывает на те органы, клетки которых интенсивно размножаются, в частности на органы кроветворения. Поражение радоном вызывает кровоизлияния, развитие злокачественных опухолей в виде сарком, рака легких, кожи и др. Установлено, что доза радона, предельно допустимая для человека, не должна превышать 0,003 рентгена в сутки. Эта доза в 10 раз меньше предельной дозы β— и γ-излучений.

Через 60—30 мин после введения в кровь кролика 10—130 мккюри радона в ней резко падает число лейкоцитов. Вслед за тем поражаются лимфатические узлы и селезенка, в меньшей мере — костный мозг. Эритроциты почти не изменяются. При периодическом вдыхании воздуха, содержащего 1 мккюри/л радона, мыши погибают через несколько недель. В организме человека радон и активные продукты его распада задерживаются на многие часы.

Прежде, когда вред, причиняемый здоровью радиоактивностью, был мало известен, у рудокопов урановых рудников Иоахимсталя (Чехия) отмечалось большое число случаев рака легких или бронхов. Радиоактивность воздуха этих рудников колебалась в пределах 3 • 10⁻⁹— 1,6•10⁻⁸ кюри/л. По советскому законодательству в воздухе населенных пунктов концентрация радона не должна превышать 3 • 10⁻¹² , а в воздухе рабочих помещений — при добыче и переработке урано-радиевых и ториевых руд, приготовлении радоновых ванн и т. д. — 3•10⁻¹¹ кюри/л. Уникален столь низкий предел допустимого содержания токсического вещества в воздухе.

На предприятиях горнорудной промышленности применяется целый комплекс мероприятий по снижению радиоактивности воздуха.

Статья на тему Радон химические свойства

Таблица Менделеева online — Rn

Все изотопы радона радиоактивны. Наиболее стабильным является изотоп ²²²Rn, являющийся дочерним продуктом распада изотопа радия ²²⁶Ra. Изотоп ²²²Rn претерпевает α-распад с периодом полураспада 3,823 дня.

В химии изотопы радона часто называют эманациями.

Исторические названия некоторых изотопов радона

Актинон (An), эманация актиния — ²¹⁹Rn.

Торон (Tn), эманация тория (ThEm) — ²²⁰Rn.

Радон (Rn), эманация радия — ²²²Rn (название совпадает с названием элемента).

В настоящее время известно 35 изотопов радона с массовыми числами от 195 до 229 и периодами полураспада от 10⁻⁶ с до 3,8 сут. Четыре изотопа радона встречаются в природе, входя в природные радиоактивные ряды: ²²²Rn и ²¹⁸Rn входят в ряд ²³⁸U, ²²⁰Rn — в ряд ²³²Th, ²¹⁹Rn — в ряд ²³⁵U. Эти природные изотопы являются дочерними продуктами альфа-распада изотопов радия (за исключением ²¹⁸Rn, возникающего в редкой боковой ветви ряда при бета-распаде ²¹⁸At) и сами в свою очередь испытывают альфа-распад, образуя изотопы полония.

Лёгкие изотопы радона (²⁰⁸Rn — ²¹²Rn) синтезируют в реакциях глубокого расщепления ядер урана или тория частицами (в основном протонами) высокой энергии или по реакциям типа ¹⁹⁷Au(¹⁴N,xn), где х — число нейтронов (обычно больше трёх).

Изотоп радона	Z(p)	N(n)	Атомная масса (u)	Период полураспада	спин ядра
Изотоп радона	Энергия возбуждения			Период полураспада	спин ядра
¹⁹⁵Rn	86	109	195,00544(5)	6 мсек	3/2-#
^195mRn	50(50) keV			6 мсек	13/2+#
¹⁹⁶Rn	86	110	196,002115(16)	4,7(11) мсек [4,4(+13-9) мсек]	0+
¹⁹⁷Rn	86	111	197,00158(7)	66(16) мсек [65(+25-14) мсек]	3/2-#
^197mRn	200(60)# keV			21(5) мсек [19(+8-4) мсек]	(13/2+)
¹⁹⁸Rn	86	112	197,998679(14)	65(3) мсек	0+
¹⁹⁹Rn	86	113	198,99837(7)	620(30) мсек	3/2-#
^199mRn	180(70) keV			320(20) мсек	13/2+#
²⁰⁰Rn	86	114	199,995699(14)	0,96(3) сек	0+
²⁰¹Rn	86	115	200,99563(8)	7,0(4) сек	(3/2-)
^201mRn	280(90)# keV			3,8(1) сек	(13/2+)
²⁰²Rn	86	116	201,993263(19)	9,94(18) сек	0+
²⁰³Rn	86	117	202,993387(25)	44,2(16) сек	(3/2-)
^203mRn	363(4) keV			26,7(5) сек	13/2(+)
²⁰⁴Rn	86	118	203,991429(16)	1,17(18) мин	0+
²⁰⁵Rn	86	119	204,99172(5)	170(4) сек	5/2-
²⁰⁶Rn	86	120	205,990214(16)	5,67(17) мин	0+
²⁰⁷Rn	86	121	206,990734(28)	9,25(17) мин	5/2-
^207mRn	899,0(10) keV			181(18) мксек	(13/2+)
²⁰⁸Rn	86	122	207,989642(12)	24,35(14) мин	0+
²⁰⁹Rn	86	123	208,990415(21)	28,5(10) мин	5/2-
^209m1Rn	1173,98(13) keV			13,4(13) мксек	13/2+
^209m2Rn	3636,78(23) keV			3,0(3) мксек	(35/2+)
²¹⁰Rn	86	124	209,989696(9)	2,4(1) ч	0+
^210m1Rn	1690(15) keV			644(40) нсек	8+#
^210m2Rn	3837(15) keV			1,06(5) мксек	(17)-
^210m3Rn	6493(15) keV			1,04(7) мксек	(22)+
²¹¹Rn	86	125	210,990601(7)	14,6(2) ч	1/2-
²¹²Rn	86	126	211,990704(3)	23,9(12) мин	0+
²¹³Rn	86	127	212,993883(6)	19,5(1) мсек	(9/2+)
²¹⁴Rn	86	128	213,995363(10)	0,27(2) мксек	0+
^214mRn	4595,4 keV			245(30) нсек	(22+)
²¹⁵Rn	86	129	214,998745(8)	2,30(10) мксек	9/2+
²¹⁶Rn	86	130	216,000274(8)	45(5) мксек	0+
²¹⁷Rn	86	131	217,003928(5)	0,54(5) мсек	9/2+
²¹⁸Rn	86	132	218,0056013(25)	35(5) мсек	0+
²¹⁹Rn	86	133	219,0094802(27)	3,96(1) сек	5/2+
²²⁰Rn	86	134	220,0113940(24)	55,6(1) сек	0+
²²¹Rn	86	135	221,015537(6)	25,7(5) мин	7/2(+)
²²²Rn	86	136	222,0175777(25)	3,8235(3) дней	0+
²²³Rn	86	137	223,02179(32)#	24,3(4) мин	7/2
²²⁴Rn	86	138	224,02409(32)#	107(3) мин	0+
²²⁵Rn	86	139	225,02844(32)#	4,66(4) мин	7/2-
²²⁶Rn	86	140	226,03089(43)#	7,4(1) мин	0+
²²⁷Rn	86	141	227,03541(45)#	20,8(7) сек	5/2(+#)
²²⁸Rn	86	142	228,03799(44)#	65(2) сек	0+
²²⁹Rn	86	143	229,0426536(141)	12 сек

Преобразование Радона — Википедия. Что такое Преобразование Радона

Двумерное преобразование Радона

Двумерное преобразование Радона.
В данном случае R(s,α) есть интеграл от f(x,y) вдоль прямой AA^‘

R(s,α)=∫−∞∞f(scos⁡α−zsin⁡α,ssin⁡α+zcos⁡α)dz{\displaystyle R(s,\alpha )=\int \limits _{-\infty }^{\infty }f(s\cos \alpha -z\sin \alpha ,s\sin \alpha +z\cos \alpha )dz} (1)

Связь преобразования Радона и преобразования Фурье. Формула обращения

Рассмотрим двумерное преобразование Фурье от функции f(x,y){\displaystyle f(x,y)}

F(kx,ky)=∫−∞∞∫−∞∞f(x,y)e−i(kxx+kyy)dxdy{\displaystyle F(k_{x},k_{y})=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(x,y)e^{-i(k_{x}x+k_{y}y)}dxdy} (2)

т.е.

F(ωcos⁡α,ωsin⁡α)=∫−∞∞e−iωsR(s,α)ds{\displaystyle F(\omega \cos \alpha ,\omega \sin \alpha )=\int \limits _{-\infty }^{\infty }e^{-i\omega s}R(s,\alpha )ds} (3)

Формула обращения для двумерного преобразования Фурье, как известно, выглядит следующим образом

Для наших целей удобно переписать эту формулу в полярных координатах

что, учитывая (3), немедленно даёт формулу обратного преобразования Радона

где R~(ω,α)=∫−∞∞R(s,α)e−iωsds{\displaystyle {\tilde {R}}(\omega ,\alpha )=\int \limits _{-\infty }^{\infty }R(s,\alpha )e^{-i\omega s}ds}.

Теорема о центральном сечении

Применим операцию прямого преобразования Фурье к преобразованию Радона от f(x,y){\displaystyle f(x,y)}:

Применение преобразования Радона

Схема получения рентгеновской томограммы

Преобразования Радона подобным образом используются и в магнито-резонансной томографии^[3].

Преобразование Радона для функции произвольного числа переменных

R(s,n→)=∫δ(n→r→−s)f(r→)dr→{\displaystyle R(s,{\vec {n}})=\int \delta ({\vec {n}}{\vec {r}}-s)f({\vec {r}})d{\vec {r}}} (2)

Обращение многомерного преобразования Радона

В многомерном случае преобразование Радона достаточно хорошей функции тоже обратимо. Покажем это.

Рассмотрим преобразование Фурье от R(s,n→){\displaystyle R(s,{\vec {n}})} по переменной s{\displaystyle s}, то есть

∫R(s,n→)e−isωds{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds}.

Используя формулу (2) и свойства дельта-функции мы получим

∫R(s,n→)e−isωds=∫f(r→)e−ir→n→ωdr→{\displaystyle \int R(s,{\vec {n}})e^{-is\omega }ds=\int f({\vec {r}})e^{-i{\vec {r}}{\vec {n}}\omega }d{\vec {r}}}.

Используя это представление векторной дельта-функции, получаем формулу обращения

Смотри также

Примечания

↑ J. Radon. Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten // Berichte Sächsische Akademie der Wissenschaften, Bande 29, s. 262-277, Leipzig, 1917.
↑ Глава 1 (недоступная ссылка)
↑ S.R. Deans, S.Roderick «The Radon Transform and Some of its Applications» Wilwy, New York, 1983 (англ.)

Ссылки

И.С.Грузман Математические задачи компьютерной томографии. Соросовский образовательный журнал No. 5, 2001 ^pdf^{txt (недоступная ссылка)}
Deans, Stanley R., The Radon Transform and Some of Its Applications. New York: John Wiley & Sons, 1983.
Natterer, Frank, The Mathematics of Computerized Tomography (Classics in Applied Mathematics, 32), Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-493-1
Natterer, Frank and Frank Wubbeling, Mathematical Methods in Image Reconstruction. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001 ISBN 0-89871-472-9

Радона формула: Преобразование Радона — Википедия – XuMuK.ru — РАДОН — Химическая энциклопедия

Преобразование Радона — Википедия

Связь преобразования Радона и преобразования Фурье. Формула обращения[править | править код]

Теорема о центральном сечении[править | править код]

Преобразование Радона для функции произвольного числа переменных[править | править код]

Обращение многомерного преобразования Радона[править | править код]

Радон

История открытия и происхождение названия

Получение

Физические свойства

Химические свойства

Преобразование Радона — Википедия

Двумерное преобразование Радона

Связь преобразования Радона и преобразования Фурье. Формула обращения

Теорема о центральном сечении

Применение преобразования Радона

Преобразование Радона для функции произвольного числа переменных

Обращение многомерного преобразования Радона

Смотри также

Примечания

Ссылки

См. также

Преобразование Радона — это… Что такое Преобразование Радона?

Двумерное преобразование Радона

Связь преобразования Радона и преобразования Фурье. Формула обращения

Теорема о центральном сечении

Применение преобразования Радона

Преобразование Радона для функции произвольного числа переменных

Обращение многомерного преобразования Радона

Примечания

Ссылки

См. также

Радон химические свойства — Знаешь как

Таблица Менделеева online — Rn

Преобразование Радона — Википедия. Что такое Преобразование Радона

Двумерное преобразование Радона

Связь преобразования Радона и преобразования Фурье. Формула обращения

Теорема о центральном сечении

Применение преобразования Радона

Преобразование Радона для функции произвольного числа переменных

Обращение многомерного преобразования Радона

Смотри также

Примечания

Ссылки

См. также

Добавить комментарий Отменить ответ