Канторова лестница – Канторова лестница — Википедия. Что такое Канторова лестница

Канторова лестница — это… Что такое Канторова лестница?

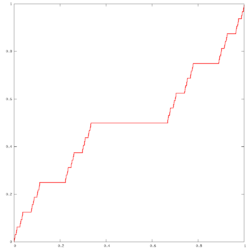Канторова лестница

Канторова лестница — пример непрерывной монотонной функции , которая не является константой, но при этом имеет производную, равную нулю в почти всех точках (сингулярной функции). Иногда называется «Чёртовой лестницей».^[1]

Построения

Стандартное

В точках 0 и 1 значение функции принимается равным соответственно 0 и 1. Далее интервал (0, 1) разбивается на три равные части , и . На среднем сегменте полагаем . Оставшиеся два сегмента снова разбиваются на три равные части каждый, и на средних сегментах полагается равной и . Каждый из оставшихся сегментов снова делится на три части, и на внутренних сегментах определяется как постоянная, равная среднему арифметическому между соседними, уже определенными значениями . На остальных точках единичного отрезка определяется по непрерывности. Полученная функция называется канторовой лестницей

.

По двоичной и троичной записи

Любое число можно представить в троичной системе счисления , . Если в записи встречается 1, выбросим из неё все последующие цифры и в оставшейся последовательности заменим каждую двойку на 1. Получившаяся последовательность даёт запись значения канторовой лестницы в точке в двоичной системе счисления.

Свойства

См. также

Ссылки

1. ↑ Weisstein, Eric W. Devil’s Staircase (англ.) на сайте Wolfram MathWorld.

Википедия — свободная энциклопедия

Избранная статья

Американская экспедиция на К2 1953 года (англ. 1953 American Karakoram expedition) — американская экспедиция на вершину Чогори под руководством доктора Чарльза Хьюстона, состоявшаяся летом 1953 года и ставившая своей целью первое восхождение на второй по высоте восьмитысячник планеты. Это была пятая по счёту попытка восхождения на К2 и третья со стороны американских альпинистов.

Экспедиция вылетела из Нью-Йорка в Карачи 25 мая 1953 года и после почти месячного перехода к Базовому лагерю у подножия К2 начала свою работу на горе. За чуть менее чем полтора месяца осады ребра Абруццкого (Абруцци) были организованы восемь промежуточных лагерей. В последнем из них (на высоте 7770 м) 2 августа собрались все участники экспедиции, готовясь к финальному рывку. Однако в ночь на 3 августа на гору обрушился шторм, который не утихал последующие две недели. На пятые сутки пережидания непогоды неожиданно тяжело заболел один из сильнейших участников экспедиции Арт Гилки, которому требовалась немедленная эвакуация вниз, но альпинисты смогли её начать лишь 10 августа. Вечером того же дня Арт Гилки погиб в результате схода снежной лавины, но, даже не имея «на руках» больного, все альпинисты смогли спуститься в Базовый лагерь только 15 августа, претерпев все возможные испытания.

Хотя экспедиция не достигла своей главной цели, в альпинистских кругах на десятилетия вперёд она стала эталоном альпинистской взаимовыручки и, по словам Райнхольда Месснера, «самой потрясающей неудачей, которую только можно себе представить».

Хорошая статья

Солове́цкий ка́мень в Санкт-Петербурге — памятник жертвам политических репрессий в СССР и борцам за свободу. Он находится на Петроградской стороне в историческом центре города, на его старейшей площади — Троицкой. Этот сквер расположен рядом с местами, непосредственно связанными с политическими репрессиями в СССР — Домом политкаторжан, тюрьмой и некрополем Петропавловской крепости, Большим домом.

Памятник представляет собой гранитную глыбу, привезённую с территории бывшего Соловецкого лагеря, считающегося символом ГУЛАГа и советского государственного террора в целом. Он был установлен по инициативе и силами бывших политических заключённых и Санкт-Петербургской организации «Мемориал». Авторами памятника выступили художники Юлий Рыбаков и Евгений Ухналёв, которые в советское время сами пережили политическое заключение. Мемориал призван увековечить память не только о жертвах репрессивной системы и о борцах с ней, но в широком смысле он символизирует ценность свободы, прав человека и человеческого достоинства. Соловецкий камень является центральным местом мероприятий, посвящённых памяти жертв государственного террора в СССР, а также других правозащитных акций.

Изображение дня

«Дрозд-отшельник» — один из геоглифов Наски

Обсуждение:Канторова лестница — Википедия

Материал из Википедии — свободной энциклопедии

Infovarius, что Вы пытаетесь «востанавить» — в вашей правке нет новой информации (хотя ошибок больше нет) но зачем-то всё переписано в три раза длиннее и с повторениям… В данном случае сделать статья становится длиннее и хуже —Тоша 19:38, 20 мая 2009 (UTC)

Точки, в которых производная канторовой лестницы не существует, образуют множество, называемое «канторовой пылью».

• Информация дублируется в свойствах — надо убрать

Это множество имеет меру нуль, хотя и состоит из несчётного числа точек, представляемых с помощью 0 и 2 в троичной системе счисления.

• Это про катнорово множество, но не про канторву лестницу — в любом случае никак не подходит для преамбулы. Остальное повторение первой фразы статьи.
• Построение: вариант infovariusа в три раза длиннее, при этом написан менее чётко.

Необычность лестницы Кантора заключается в том, что «подъём» по ней происходит на множестве меры нуль.

Длина всей лестницы равна 1:

• Что это за длина? и далее в этой секции ерунда с тривиальными подсчётами — по сути переписано очень плохо то, что множество Кантора имеет меру ноль. НО, статье про канторову лестницу а не про множество…

—Тоша 16:17, 21 мая 2009 (UTC)

Тоша, Ты мог бы пояснить что тебя побудило сделать откат моей правки? На мой взгляд мое построение дано более грамотно — подробно расписано по шагам и приведено условия предельного перехода. По поводу длины лестницы: спорный вопрос. Длина кривой существует, т.к. фукнция имеет ограниченную вариацию. Возможно вместо того, чтобы критиковать неудачное выражение имеет смысл предложить конструктивный вариант. Скажем, «сумма длин ступеней лестницы».

Далее, конкретно по текущей версии: «На остальных точках единичного отрезка определим по непрерывности» — это на каких «остальных»? ИМХО, фраза крайне неудачная. Потому как тогда нужно объяснить, что это за «остальные точки» — из статьи это совершенно не ясно. Потом, что означает «и так далее» в данном контексте? Никоим образом не поятно, что нужно делать далее — о рекурсии или индукции ни слова нет.

Balmo 19:47, 2 марта 2010 (UTC)

Например, Вы пишите «Продолжая процесс разбиения, в пределе получим функцию, называемую канторовой лестницей». Не вполне ясно, что значит «в пределе»; первое определение которое приходит в голову даёт только функцию вне канторова множества. —Тоша 17:06, 5 марта 2010 (UTC)

Совершенно стандартное выражение. Например из той же википедии: http://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BA%D1%82%D0%B0%D0%BB%D1%8B. Из классического например Фихтенгольц Г.М. «Основы мат.анализа» т.2. стр. 70 или Треногин В.А. «Функ.ан.» стр.42. Как-то странно на мой взгляд вот так, не разобравшись в сути вопроса делать отмену правок целого раздела статьи. В конце концов, если не понравилось тебе выражение — можно исправить его или попросить исправить меня. Но я думаю разберешься. Все-таки тебе виднее — как оно молодежью лучше воспринимается, выражение это. А академики и так знают что это такое и при необходимости отфильтруют всю шелуху. То и ты меня пойми правильно — мне подобные высказывания слух режут. Привык я просто, видимо, к другому стилю изложения, более строгому что ли… Balmo 19:58, 7 марта 2010 (UTC)

Выражение не должно быть стандартным, но должно быть правильным. По-моему сейчас правильнее чем было, и при этом вполне ясно и однозначно. —Тоша 01:55, 13 марта 2010 (UTC)

Я просто поражаюсь, Тоша прямо-таки горой стоит за короткую версию, при этом особенно не вникая в то, что делают другие, а просто откатывает. Замечу, что «благодаря» этим откатам, уже полгода нет необходимой ссылки на сингулярную функцию. infovarius 22:06, 13 марта 2010 (UTC)

Антон(Infovarius), Вы не правы, я очень внимательно читаю все исправления — откатываю только если становится хуже. —Тоша 04:44, 16 марта 2010 (UTC)

Хорошо, про «особенно не вникая» не прав. Но если правка на 80% плохая, то откатывая её Вы лишаете статью 20% пользы — я про это (ссылка-то пропала). infovarius 18:08, 16 марта 2010 (UTC)

Я не вредный, я полезный. Если вижу как исправить — исправляю… —Тоша 05:28, 17 марта 2010 (UTC)

• Поделюсь опытом, как можно «подкупить» Тошу: АИ! (пока проверено на 1 примере) 🙂 Fractaler 10:21, 17 марта 2010 (UTC)

Тоша писал «Выражение не должно быть стандартным, но должно быть правильным». ИМХО у Фихтенгольца было неправильно, и тридцать лет никто до Антона не замечал… 95.79.162.116 09:57, 20 марта 2010 (UTC)

«На остальных точках единичного отрезка определяется по непрерывности.» из предложения мне не понятно как она строится. Разбиение на «тройки» происходит только три раза или «до бесконечности»? Какие такие «остальные точки» имеются ввиду, мне тоже не понятно. Ткните пожалуйста. —Dnikitin 13:53, 22 декабря 2011 (UTC)

• Остальные значит те точки на отрезке, для на которых функция ещё не определена.—Тоша 23:40, 22 декабря 2011 (UTC)

А что за странные пляски с «доопределением по непрерывности»? Не проще ли сразу определять не на интервале, а на отрезке? —212.114.10.196 13:12, 15 мая 2012 (UTC)

Канторово множество — Википедия

Материал из Википедии — свободной энциклопедии

Ка́нторово мно́жество (канторов дисконтинуум, канторова пыль) — один из простейших фракталов, подмножество единичного отрезка вещественной прямой, которое является классическим примером дисконтинуума в математическом анализе. Описано в 1883 году Георгом Кантором.

Классическое построение[править | править код]

Из единичного отрезка C0=[0,1]{\displaystyle C_{0}=[0,1]} удалим среднюю треть, то есть интервал (1/3,2/3){\displaystyle (1/3,2/3)}. Оставшееся точечное множество обозначим через C1{\displaystyle C_{1}}. Множество C1=[0,1/3]∪[2/3,1]{\displaystyle C_{1}=[0,1/3]\cup [2/3,1]} состоит из двух отрезков; удалим теперь из каждого отрезка его среднюю треть, и оставшееся множество обозначим через C2{\displaystyle C_{2}}. Повторив эту процедуру опять, удаляя средние трети у всех четырёх отрезков, получаем C3{\displaystyle C_{3}}. Дальше таким же образом получаем последовательность замкнутых множеств C0⊃C1⊃C2⊃…{\displaystyle C_{0}\supset C_{1}\supset C_{2}\supset \dots }. Пересечение

C=⋂i=0∞Ci{\displaystyle C=\bigcap _{i=0}^{\infty }C_{i}}

называется канторовым множеством.

Множества C0, C1, C2, C3, C4, C5, C6{\displaystyle C_{0},\ C_{1},\ C_{2},\ C_{3},\ C_{4},\ C_{5},\ C_{6}}

С помощью троичной записи[править | править код]

Канторово множество может быть также определено как множество чисел от нуля до единицы, которые можно представить в троичной записи с помощью только нулей и двоек. При этом следует отметить, что число принадлежит канторовому множеству, если у него есть хотя бы одно такое представление, например 0,13∈C{\displaystyle 0{,}1_{3}\in C}, так как 0,13=0,0(2)3{\displaystyle 0{,}1_{3}=0{,}0(2)_{3}}.

Как аттрактор[править | править код]

Канторово множество может быть определено как аттрактор. Рассмотрим все последовательности точек {xn}{\displaystyle \{x_{n}\}} такие, что для любого n{\displaystyle n}

xn+1=xn/3{\displaystyle x_{n+1}=x_{n}/3} или xn+1−1=(xn−1)/3{\displaystyle x_{n+1}-1=(x_{n}-1)/3}.

Тогда множество пределов всех таких последовательностей является канторовым множеством.

Как счётная степень простого двоеточия[править | править код]

В литературе по общей топологии канторово множество определяется как счётная степень двухточечного дискретного пространства — {0;1}ℵ0{\displaystyle \{0;1\}^{\aleph _{0}}}^[1]; такое пространство гомеоморфно классически построенному канторову множеству (с обычной евклидовой топологией)^[2][3].

• Энгелькинг Р. . Общая топология. — М.: Мир, 1986. — 752 с.

математический-анализ / Канторово Множество / Математика

Стандартную информация о канторовом множестве и канторовой лестнице можно найти в книгах или в Сети — скажем, здесь. Каких-то особых подробностей, скорее всего, не нужно — достаточно знать основные свойства.

Прежде всего, если единичный отрезок разбить на три части, то в первую часть попадут числа, троичная запись которых имеет вид 0,0…; во вторую попадут числа с записью вида 0,1…; в третьей части окажутся числа с троичной записью вида 0,2… . Далее происходит аналогичный процесс, и в канторово множество попадают все числа, запись которых в троичной системе состоит из цифр 0 и 2, а цифра 1 при этом не участвует. Вместо 0,1 мы здесь пишем двойку в периоде: 0,02222…, чтобы это описание в точности имело место. Из сказанного следует, что канторово множество имеет ту же мощность, что и множество бесконечных последовательностей из цифр 0 и 2, то есть континуум. При этом оно нигде не плотно.

Канторова лестница, определение которой дано по ссылке, непрерывна на отрезке. Поэтому она интегрируема по Риману, и интеграл $%\int_0^1K(x)\,dx$% равен площади под графиком функции. Легко видеть, что график симметричен относительно центра единичного квадрата, поэтому он разбивает квадрат на две части равной площади. Следовательно, значение интеграла равно 1/2.

Число 9/10 можно представить в виде суммы ряда следующим образом: $%\frac9{10}=\frac23+\frac29+\frac1{90}$%, где последнее слагаемое равно $%3^{-4}\cdot\frac9{10}$%. Отсюда возникает периодичность разложения, то есть $%\frac9{10}=\frac2{3^1}+\frac2{3^2}+\frac2{3^5}+\frac2{3^6}+\cdots$%. Иными словами, это $%0,22002200…$% из нулей и двоек. Поэтому канторову множеству данное число принадлежит.

Для нахождения значения $%y=K(\frac9{10})$% нужно использовать самоподобие графика канторовой лестницы. Поскольку $%\frac9{10}=\frac23+\frac7{30}$%, получается равенство $%K(\frac9{10})=\frac12+\frac12K(\frac7{10})$%. Действительно, график функции на третьей части разбиения поднят на $%\frac12$% и сжат вдвое по оси ординат. Если мы его растянем в три раза вдоль оси абсцисс, отображая в масштабе на весь отрезок, то число $%\frac7{30}$% увеличится втрое, что и даст указанное равенство.

Далее, $%\frac7{10}$% снова принадлежит третьей части разбиения, и $%\frac7{10}=\frac23+\frac1{30}$%, откуда $%K(\frac7{10})=\frac12+\frac12K(\frac1{10})$%. Далее для чисел из первой трети последовательно будем иметь $%K(\frac1{10})=\frac12K(\frac3{10})=\frac14K(\frac9{10})=\frac14y$%. Отсюда $%K(\frac7{10})=\frac12+\frac18y$%, и $%y=\frac12+\frac14+\frac1{16}y$%. Тем самым, $%y=\frac45$%.

отвечен 17 Фев ’16 3:40

Канторова лестница — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Канторова лестница — пример непрерывной монотонной функции <math>[0,1]\to [0,1]</math>, которая не является константой, но при этом имеет производную, равную нулю в почти всех точках (сингулярной функции). Иногда называется «Чёртовой лестницей».^[1]

Построения

Стандартное

В точках 0 и 1 значение функции принимается равным соответственно 0 и 1. Далее интервал (0, 1) разбивается на три равные части <math>\left(0,\frac{1}{3}\right)</math>, <math>\left(\frac{1}{3},\frac{2}{3}\right)</math> и <math>\left(\frac{2}{3},1\right)</math>. На среднем сегменте полагаем <math>F(x) = \frac{1}{2}</math>. Оставшиеся два сегмента снова разбиваются на три равные части каждый, и на средних сегментах <math>F(x)</math> полагается равной <math>\frac{1}{4}</math> и <math>\frac{3}{4}</math>. Каждый из оставшихся сегментов снова делится на три части, и на внутренних сегментах <math>F(x)</math> определяется как постоянная, равная среднему арифметическому между соседними, уже определенными значениями <math>F(x)</math>. На остальных точках единичного отрезка определяется по непрерывности. Полученная функция называется канторовой лестницей.

По двоичной и троичной записи

Любое число <math>x\in[0,1]</math> можно представить в троичной системе счисления <math>x=(0{,}a_1a_2\dots)_3</math>, <math>a_i\in\{0,1,2\}</math>. Если в записи <math>0{,}a_1a_2\dots</math> встречается 1, выбросим из неё все последующие цифры и в оставшейся последовательности заменим каждую двойку на 1. Получившаяся последовательность <math>0{,}b_1b_2\dots</math> даёт запись значения канторовой лестницы в точке <math>x</math> в двоичной системе счисления.

Свойства

См. также

Напишите отзыв о статье «Канторова лестница»

Ссылки

1. ↑ Weisstein, Eric W. [mathworld.wolfram.com/DevilsStaircase.html Devil’s Staircase] (англ.) на сайте Wolfram MathWorld.

Отрывок, характеризующий Канторова лестница

Х
Вернувшись к караулке, Петя застал Денисова в сенях. Денисов в волнении, беспокойстве и досаде на себя, что отпустил Петю, ожидал его.
– Слава богу! – крикнул он. – Ну, слава богу! – повторял он, слушая восторженный рассказ Пети. – И чег’т тебя возьми, из за тебя не спал! – проговорил Денисов. – Ну, слава богу, тепег’ь ложись спать. Еще вздг’емнем до утг’а.
– Да… Нет, – сказал Петя. – Мне еще не хочется спать. Да я и себя знаю, ежели засну, так уж кончено. И потом я привык не спать перед сражением.
Петя посидел несколько времени в избе, радостно вспоминая подробности своей поездки и живо представляя себе то, что будет завтра. Потом, заметив, что Денисов заснул, он встал и пошел на двор.
На дворе еще было совсем темно. Дождик прошел, но капли еще падали с деревьев. Вблизи от караулки виднелись черные фигуры казачьих шалашей и связанных вместе лошадей. За избушкой чернелись две фуры, у которых стояли лошади, и в овраге краснелся догоравший огонь. Казаки и гусары не все спали: кое где слышались, вместе с звуком падающих капель и близкого звука жевания лошадей, негромкие, как бы шепчущиеся голоса.
Петя вышел из сеней, огляделся в темноте и подошел к фурам. Под фурами храпел кто то, и вокруг них стояли, жуя овес, оседланные лошади. В темноте Петя узнал свою лошадь, которую он называл Карабахом, хотя она была малороссийская лошадь, и подошел к ней.
– Ну, Карабах, завтра послужим, – сказал он, нюхая ее ноздри и целуя ее.
– Что, барин, не спите? – сказал казак, сидевший под фурой.
– Нет; а… Лихачев, кажется, тебя звать? Ведь я сейчас только приехал. Мы ездили к французам. – И Петя подробно рассказал казаку не только свою поездку, но и то, почему он ездил и почему он считает, что лучше рисковать своей жизнью, чем делать наобум Лазаря.
– Что же, соснули бы, – сказал казак.
– Нет, я привык, – отвечал Петя. – А что, у вас кремни в пистолетах не обились? Я привез с собою. Не нужно ли? Ты возьми.
Казак высунулся из под фуры, чтобы поближе рассмотреть Петю.

Лестница Кантора — это… Что такое Лестница Кантора?



Лестница Кантора

Wikimedia Foundation. 2010.

• Лестница Джейкоба (фильм)
• Лестница Якоба

Смотреть что такое «Лестница Кантора» в других словарях:

• Кантора множество — Канторово множество есть один из простейших фракталов, подмножество единичного отрезка вещественной прямой, которое является классическим примером «плохого множества» в математическом анализе. Описано в 1883 году Г. Кантором. Содержание 1… …   Википедия

• Функция Кантора — Канторова лестница Канторова лестница  пример непрерывной монотонной функции , которая не является константой, но при этом имеет производную равную нулю в почти всех точках. Построение Рассмотрим функцию, равную 1 / 2 на [1 / 3,2 / 3] …   Википедия

• Множество Кантора — Канторово множество есть один из простейших фракталов, подмножество единичного отрезка вещественной прямой, которое является классическим примером «плохого множества» в математическом анализе. Описано в 1883 году Г. Кантором. Содержание 1… …   Википедия

• Множество кантора — Канторово множество есть один из простейших фракталов, подмножество единичного отрезка вещественной прямой, которое является классическим примером «плохого множества» в математическом анализе. Описано в 1883 году Г. Кантором. Содержание 1… …   Википедия

• Теорема Лебега о разложении меры — У этого термина существуют и другие значения, см. Теорема Лебега. Вводные определения Пусть   монотонно неубывающая функция, непрерывная справа на отрезке . На вводится борелевская алгебра …   Википедия

• Кантор, Георг Фердинанд Людвиг Филипп — В Википедии есть статьи о других людях с такой фамилией, см. Кантор. Георг Кантор Georg Ferdinand Ludwig Philipp Cantor …   Википедия

• Кантор, Георг — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург …   Википедия

• Кантор, Георг Фердинанд — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург …   Википедия

• Кантор Георг — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург …   Википедия

• Кантор Георг Фердинанд — Георг Кантор Georg Ferdinand Ludwig Philipp Cantor Георг Кантор Дата рождения: 19 февраля (3 марта) 1845(18450303) Место рождения: Санкт Петербург …   Википедия